[Python] 9663 Nqueen

in Algorithm on 문제풀이, 백트래킹


9663 Nqueen

문제

N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.

N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N이 주어진다. (1 ≤ N < 15)

출력

첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.

풀이

dfs로 풀 수 있다. 하지만 모든 경우의 수를 고려한다면 N = 15일 경우 15^15로 제한시간을 넘겨버린다. 조건문을 통해 유망하지 않은 노드의 경우 다시 돌아가 다른 자식 노드를 검색하는 백트래킹 알고리즘을 이용해야한다. 유망성 검증을 위해 다음 4가지를 구현해야 한다.

  1. 해당 row에 이미 놓여진 말이 있는지
  2. 해당 col에 이미 놓여진 말이 있는지
  3. 오른쪽 위의 대각선 방향으로 이미 놓여진 말이 있는지
  4. 오른쪽 아래의 대각선 방향으로 이미 놓여진 말이 있는지

1번 2번의 경우

row와 col상태는 방문상태를 체크하면 되므로 큰 문제가 없다.

3번의 경우

row와 col을 더한 값을 체크하면 된다. 아래 그림처럼 해당 대각선에 있는 좌표들의 합은 모두 2이다. 즉 row+col의 방문상태를 체크하면 된다.

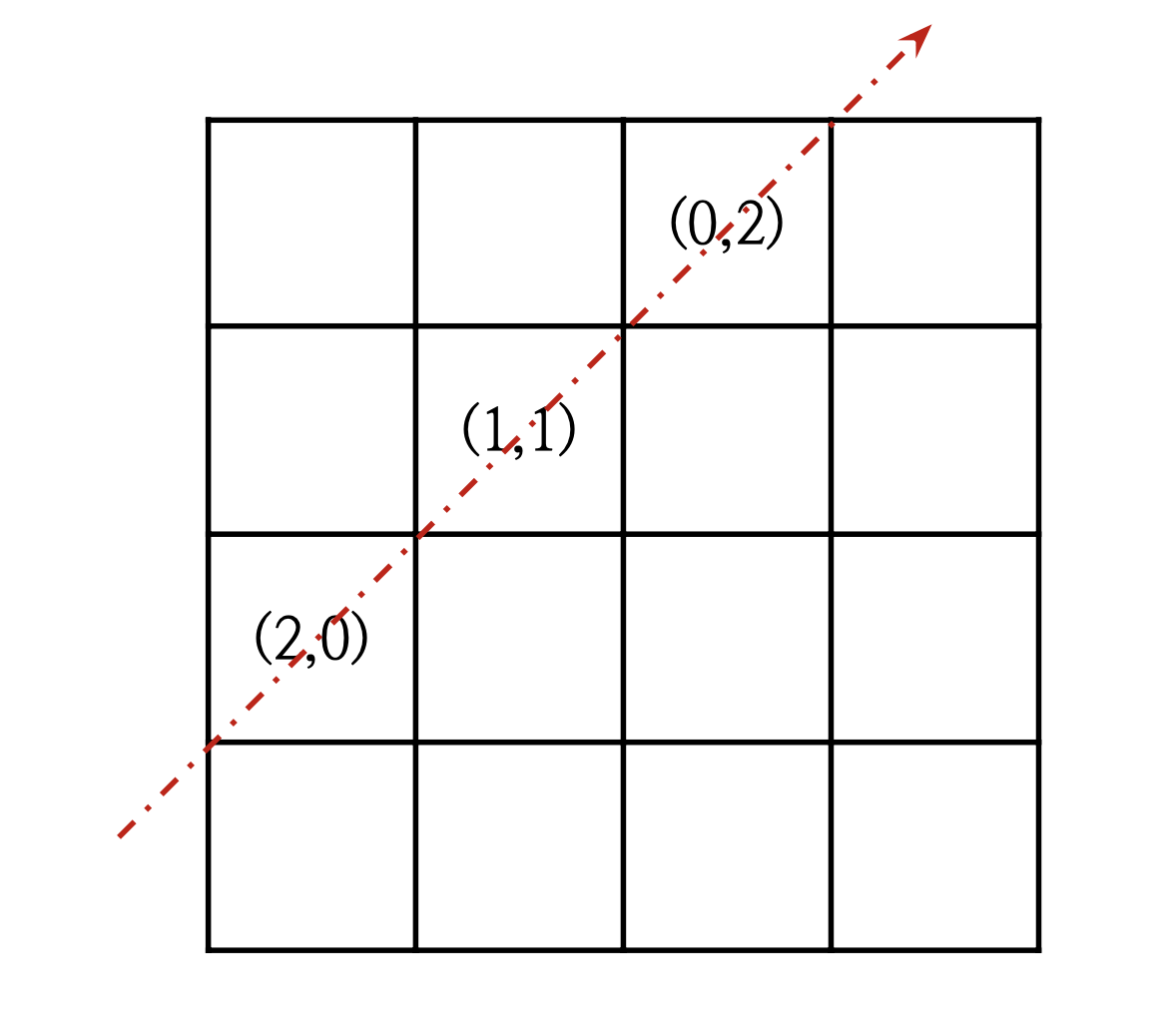
nqueen1

4번의 경우

아래 그림처럼 해당 대각선에서 row-column은 모두 1이다. 즉 row-col의 방문상태를 체크하면 된다. 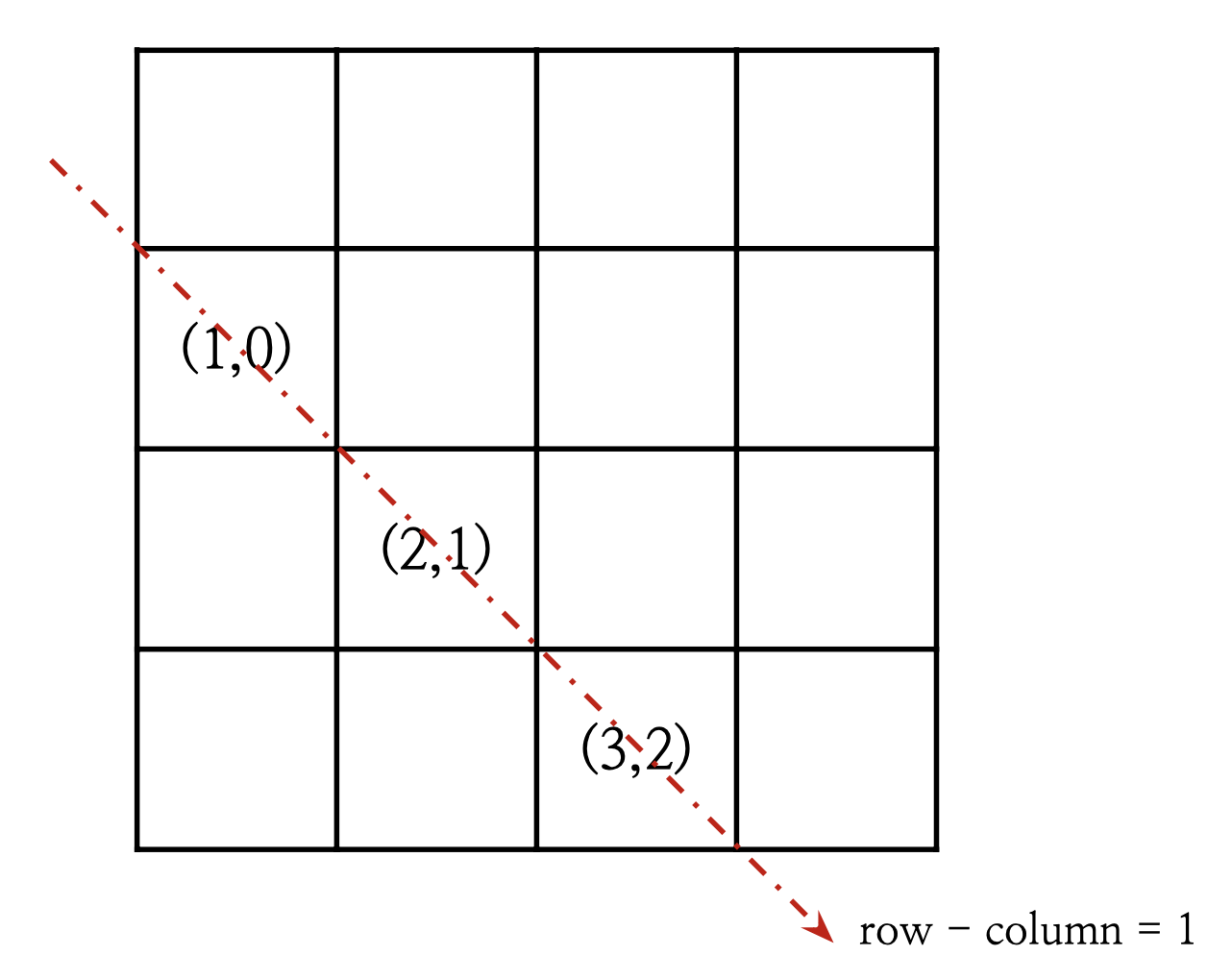nqueen2

n = int(input())

answer = 0
col = set()
diagonal1 = set()
diagonal2 = set()

def dfs(n,row,col,diagonal1, diagonal2):
    global answer
    if row==n:
        answer += 1
        return

    for hubo in range(n): # 매 row마다 가능한 col을 탐색
        if (hubo in col) or (row+hubo in diagonal1) or (row-hubo in diagonal2):
            continue

        col.add(hubo)
        diagonal1.add(row+hubo)
        diagonal2.add(row-hubo)

        dfs(n,row+1,col,diagonal1,diagonal2)

        col.remove(hubo)
        diagonal1.remove(row+hubo)
        diagonal2.remove(row-hubo)

def solution(n):
    dfs(n, 0, col, diagonal1, diagonal2)
    return answer

print(solution(n))