9084 동전

문제

우리나라 화폐단위, 특히 동전에는 1원, 5원, 10원, 50원, 100원, 500원이 있다. 이 동전들로는 정수의 금액을 만들 수 있으며 그 방법도 여러 가지가 있을 수 있다. 예를 들어, 30원을 만들기 위해서는 1원짜리 30개 또는 10원짜리 2개와 5원짜리 2개 등의 방법이 가능하다.

입력

입력의 첫 줄에는 테스트 케이스의 개수 T(1 ≤ T ≤ 10)가 주어진다. 각 테스트 케이스의 첫 번째 줄에는 동전의 가지 수 N(1 ≤ N ≤ 20)이 주어지고 두 번째 줄에는 N가지 동전의 각 금액이 오름차순으로 정렬되어 주어진다. 각 금액은 정수로서 1원부터 10000원까지 있을 수 있으며 공백으로 구분된다. 세 번째 줄에는 주어진 N가지 동전으로 만들어야 할 금액 M(1 ≤ M ≤ 10000)이 주어진다.

편의를 위해 방법의 수는 2^31 - 1 보다 작고, 같은 동전이 여러 번 주어지는 경우는 없다.

출력

각 테스트 케이스에 대해 입력으로 주어지는 N가지 동전으로 금액 M을 만드는 모든 방법의 수를 한 줄에 하나씩 출력한다.

풀이

처음에는 DFS로 완전탐색으로 풀었으나 시간초과가 떴다. 동전의 가지수는 최대 20개로 20개의 depth를 가지고 매 depth별로 M // coin번 탐색해야 하므로 최대 10000 * 5000 * …으로 내려가 1억 computation을 넘긴다. 즉, 제한시간 1초내에 풀 수 없다.

다음, DP로 접근을 해보았다. coin이 2,3,5가 있고 M=10이라고 가정해보자.

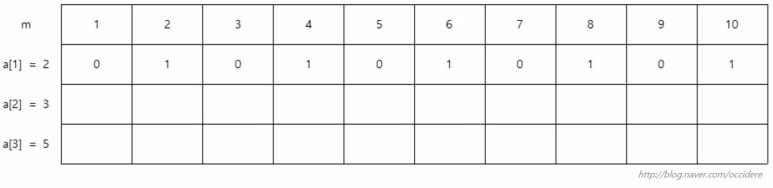
첫번째 경우인 2원을 가지고 목표금액인 10원까지 만드는 경우는 이렇게 끝난다. m=2일때 2원 동전이 한개 필요하다면 m=4일때는 m=2에서 2원짜리 동전을 추가해주면 된다.

즉, m[i][j] += m[i][j-coin[i]]가 된다.

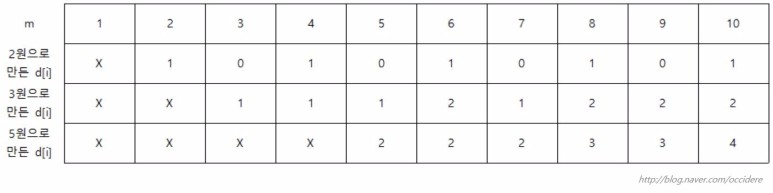
다음은 3원과 5원의 경우도 추가한 것이다. m=6일때 2원으로만 만드는 경우는 1가지(2원*3개)이다. 3원으로 만들 수 있는 경우를 보자. 3원을 사용하지 않는 2원만 사용하는 경우를 더해줘야 한다.

즉, m[i][j] += m[i-1][j]가 된다.

정리해보면 전체 점화식은 다음과 같다.

m[i][j] = m[i][j-coin[i]]+m[i-1][j]

다만 이때 j가 coin[i]보다 클때만 m[i][j-coin[i-1]]을 더해주도록 한다.

T = int(input())
for i in range(T):
    N = int(input())
    coin = list(map(int, input().split()))
    M = int(input())
    dp = [[0]*(M+1) for _ in range(len(coin)+1)]

    for i in range(len(coin)+1):
        dp[i][0] = 1

    for i in range(1, len(coin)+1):
        for j in range(1, M+1):
            if j >= coin[i-1]:
                dp[i][j] = dp[i-1][j] + dp[i][j-coin[i-1]]
            else:
                dp[i][j] = dp[i-1][j]

    print(dp[-1][-1])