21943 최단경로

문제

N개의 양의 정수 X 와 곱하기 연산자, 더하기 연산자가 총 N-1 개가 존재하고 괄호는 무수히 많이 사용해도 된다. 이 연산에는 곱하기 연산자와 더하기 연산자의 우선순위가 동일하다.

정수와 연산자는 아래와 같이 배치해야 한다. 정수의 순서는 바꿔도 상관없다.

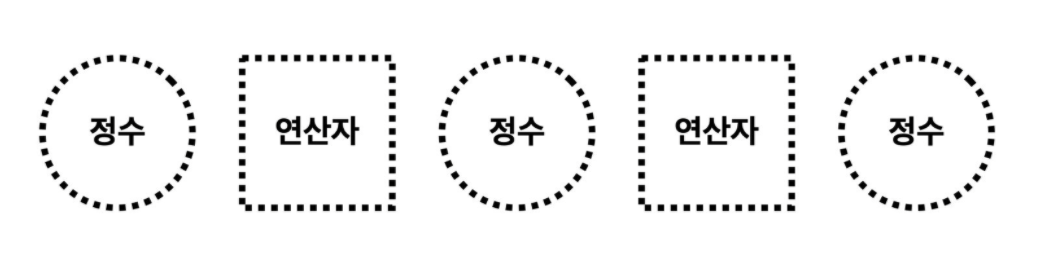
예를 들어 1,2,3이 있고 더하기 연산자와 곱하기 연산자가 각각 하나 있다고 가정하면 아래와 같이 만들 수 있다.

예를 들어 1,2,3,4,5,6,7,8와 더하기 연산자가 4개 곱하기 연산자가 1개 있다고 하자. 괄호를 이용하여 최대값을 구하는 방법 중 일부이다.

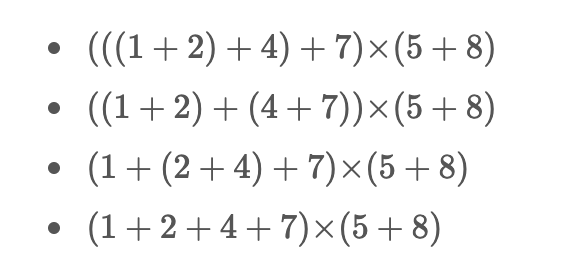
연산을 잘 이용하여 값을 최대로 만들어 보자

입력

첫째 줄에 입력될 양의 정수 개수를 뜻하는 N이 주어진다.

그 다음줄에는 N 개의 양의 정수 X 가 공백으로 구분되어 주어진다.

마지막 줄에는 더하기 연산자의 개수 P와 곱하기 연산자의 개수 Q가 공백으로 구분되어 주어진다.

출력

가능한 연산의 결과 중 최댓값을 출력한다.

풀이

• Greedy 문제입니다. 곱셈 연산 전에 덧셈 연산을 미리 하는 것이 최댓값이 됩니다.

• 괄호를 나누는 것은 곧 Q+1개의 부분집합으로 나누는 것으로 이를 dfs로 구현하였습니다.

• 주어진 숫자가 정렬될 수 있는 모든 경우의 수를 나열한 후 dfs로 다시 괄호가 놓일 수 있는 모든 경우의 수를 찾습니다.

• 괄호 안의 부분집합의 덧셈을 모두 곱하는 것이 최댓값 후보이고 이들 중 가장 큰 값을 출력합니다.

import sys
from itertools import permutations

max_v = -sys.maxsize

N = int(input())
my_list = list(map(int, input().split()))
P, Q = map(int, input().split())

def dfs(my_list, q, answer): # q개의 집합으로 분리
    global max_v
    if q == 1:
        if answer*sum(my_list) > max_v:
            max_v = answer*sum(my_list)
        return
    for i in range(1, len(my_list)-q+2):
        dfs(my_list[i:], q-1, answer*sum(my_list[:i]))

result = list(permutations(my_list,len(my_list)))
result = set(result)

for a in result:
    dfs(a,Q+1,1)

print(max_v)