프로그래머스 섬 연결하기

문제

n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.

다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.

제한사항

• 섬의 개수 n은 1 이상 100 이하입니다.
• costs의 길이는 ((n-1) * n) / 2이하입니다.
• 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
• 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
• 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
• 연결할 수 없는 섬은 주어지지 않습니다.

입출력 예

입출력 예 설명

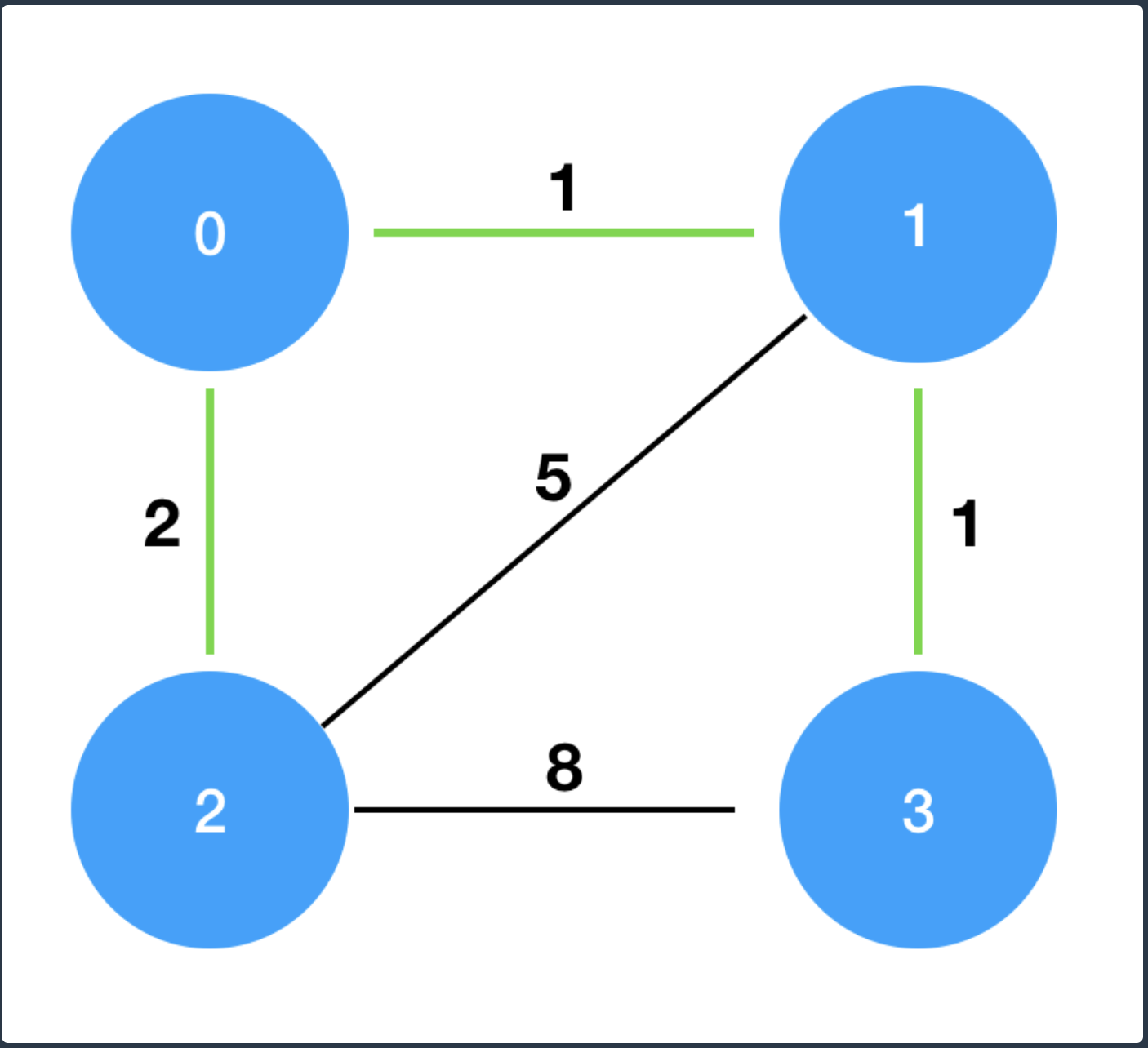
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.

풀이

• 크루스칼 알고리즘을 이용하여 풀 수 있습니다.
• costs에는 간선 정보와 비용이 들어있으므로 먼저 비용으로 정렬합니다.
• 적은 비용의 간선부터 차례로 연결시켜주면서 union-find 알고리즘을 통해 싸이클이 형성되는 경우는 제외합니다.
• 연결이 되는 경우에만 비용을 차례로 더해주고 마지막에 최종 비용을 return 합니다.

def solution(n,costs):
    def find(u): ## u 정점의 루트 노드 탐색
        if u != p[u]: ## u가 루트 노드가 아니면
            p[u] = find(p[u]) # 3 -> 2, 2 -> 1 일 경우 3 -> 1 로 경로 압축
        return p[u] ## u가 루트 노트이면 u 반환

    def union(u, v):
        root1 = find(u) # B'
        root2 = find(v)  # A'
        p[root2] = root1 # A'의 부모느드를 B'로 변경

    costs.sort(key = lambda x: x[2])
    p = [0] # 상호배타적 집합
    tree_edges = 0 # 간선 개수
    mst_cost = 0  # 가중치 합

    for i in range(1, n+1):
        p.append(i)

    while True:
        if tree_edges == n-1:
            break
        u, v, wt= costs.pop(0)
        if find(u) != find(v): # 두 노드의 루트 노드가 다르다면 두 노드가 포함되어 있는 집합을 하나로 결합
            union(u,v)
            mst_cost += wt
            tree_edges += 1
    return mst_cost