[Algorithm] 힙(heap) 이란?
in Algorithm on DataStructure, Heap
1. 자료구조 힙(Heap)이란?
- 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.
- 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
- 힙은 일종의 반 정렬 상태(느슨한 정렬 상태)를 유지한다.
- 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
- 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은)이진 트리를 말한다.
- 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
2 .힙의 종류
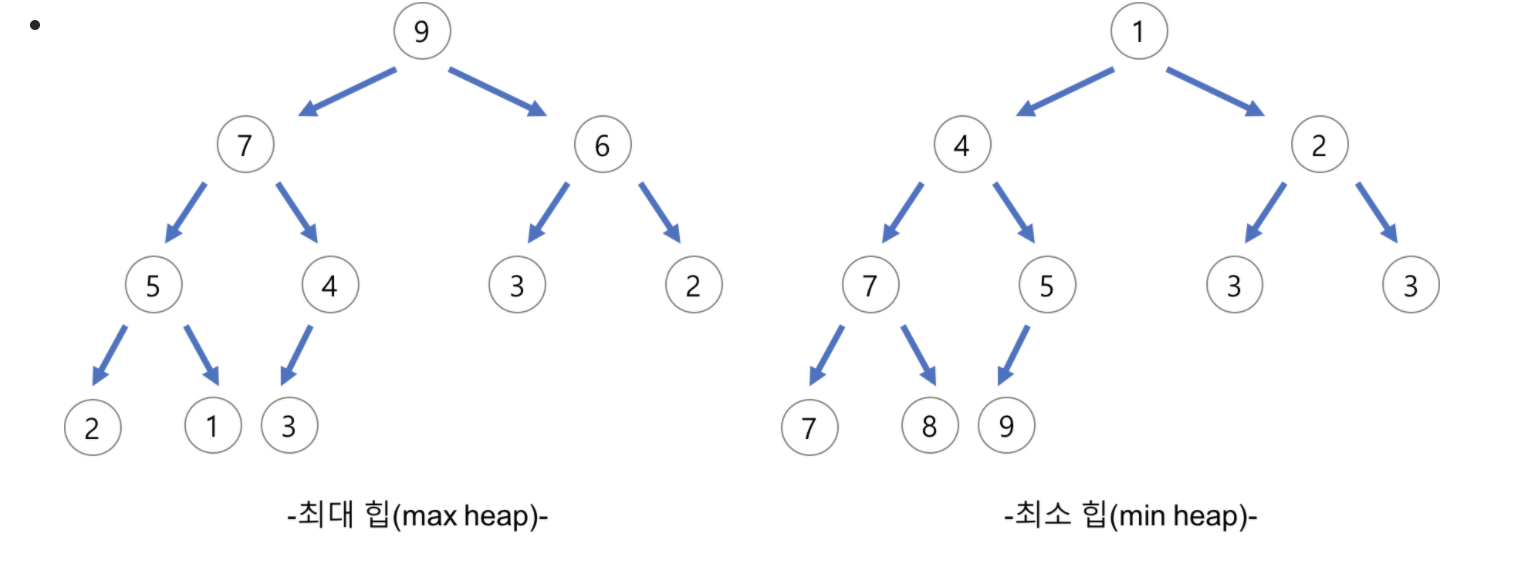
- 최대 힙(max heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- key(부모 노드) >= key(자식 노드)
- 최소 힙(min heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
- key(부모 노드) <= key(자식 노드)
3. 힙(heap) 구현
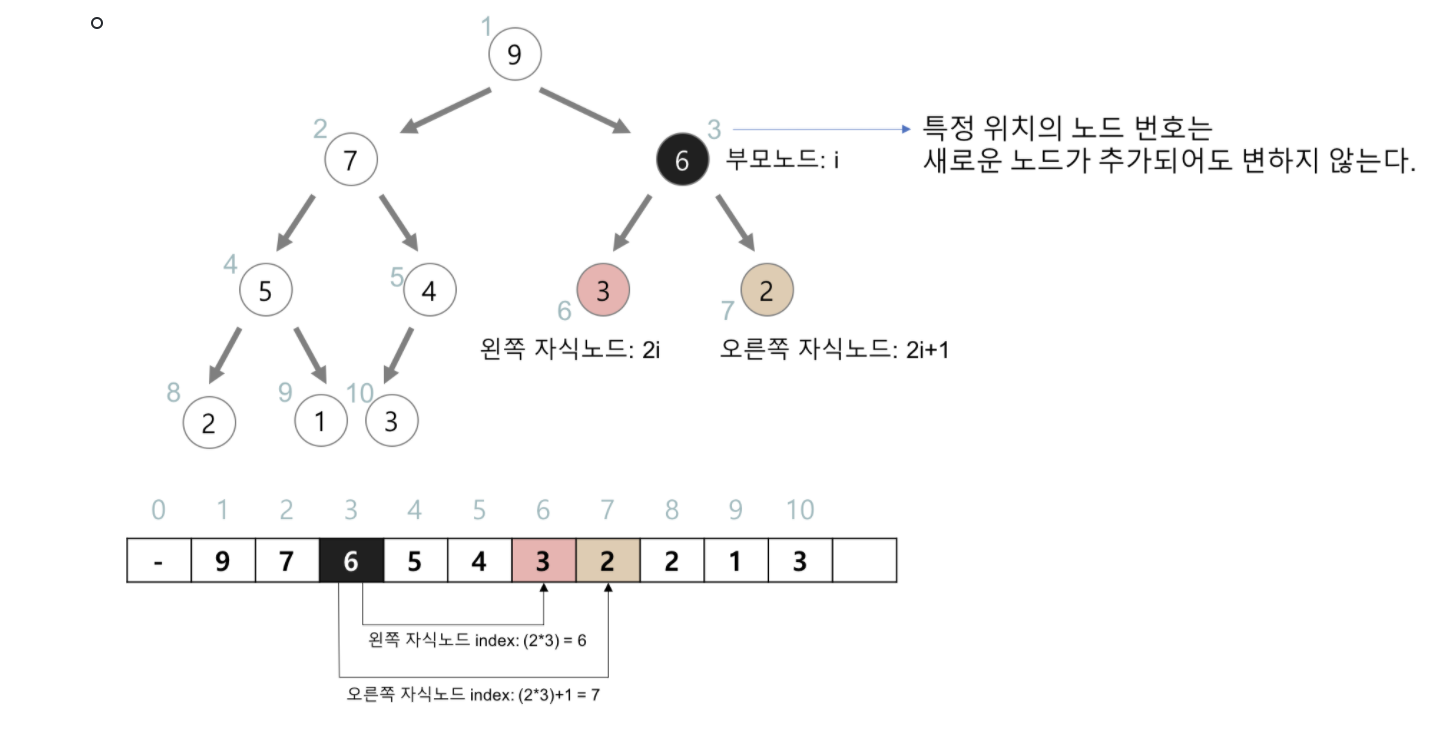
- 힙을 저장하는 표준적인 자료구조는 배열이다
- 구현을 쉽게 하기 위하여 배열의 첫 번째 인덱스인 0은 사용되지 않는다.
- 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
- 예를 들어 루트 노드의 오른쪽 노드의 번호는 항상 3이다.
- 힙에서의 부모 노드와 자식 노드의 관계
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 시간복잡도: O(N)
4. 힙(heap) 삽입
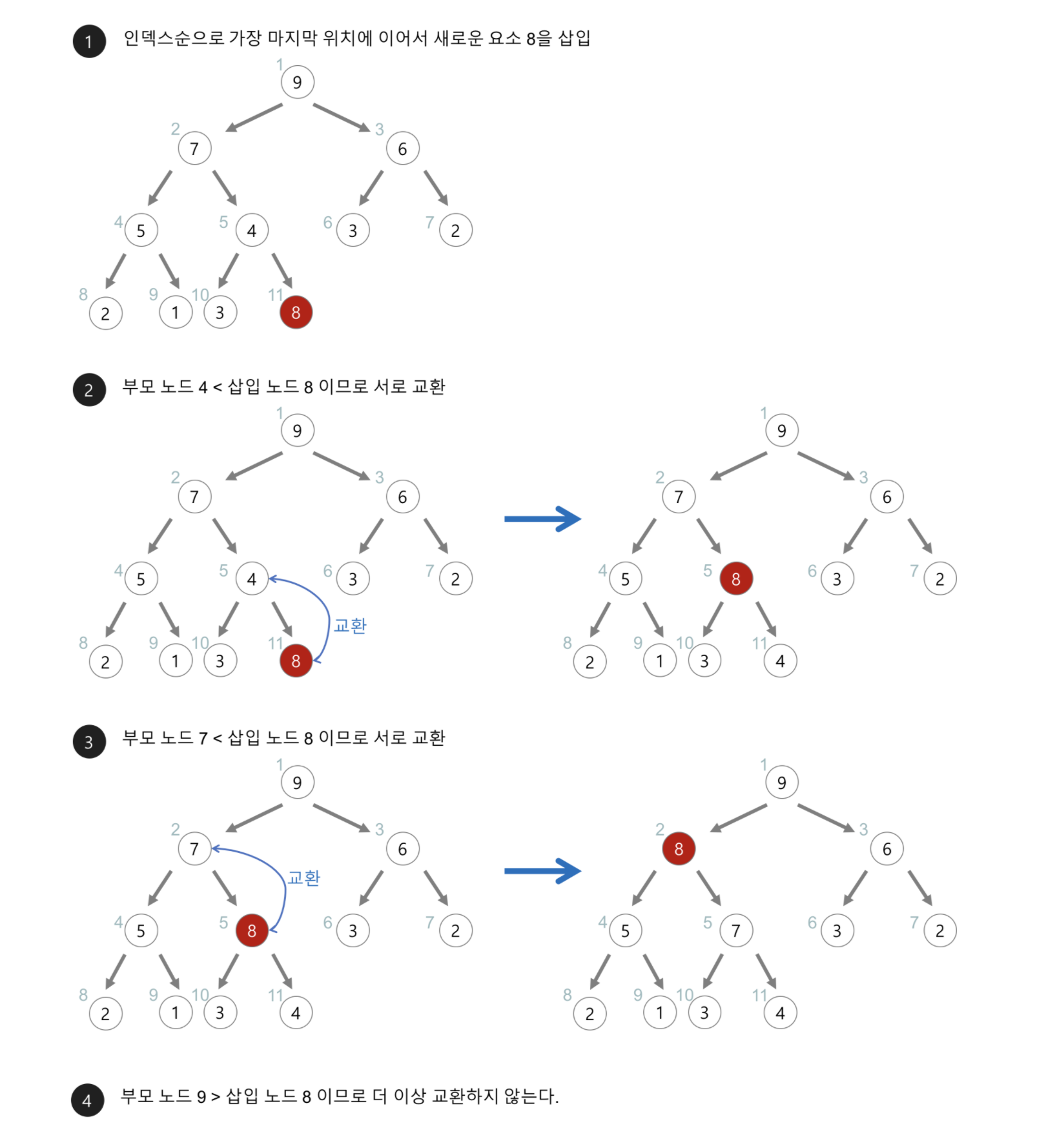
- 합에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
- 아래의 최대 힙(max heap)에 새로운 요소 8을 삽입
- 시간 복잡도: O(logN)
5. 힙(heap)의 삭제
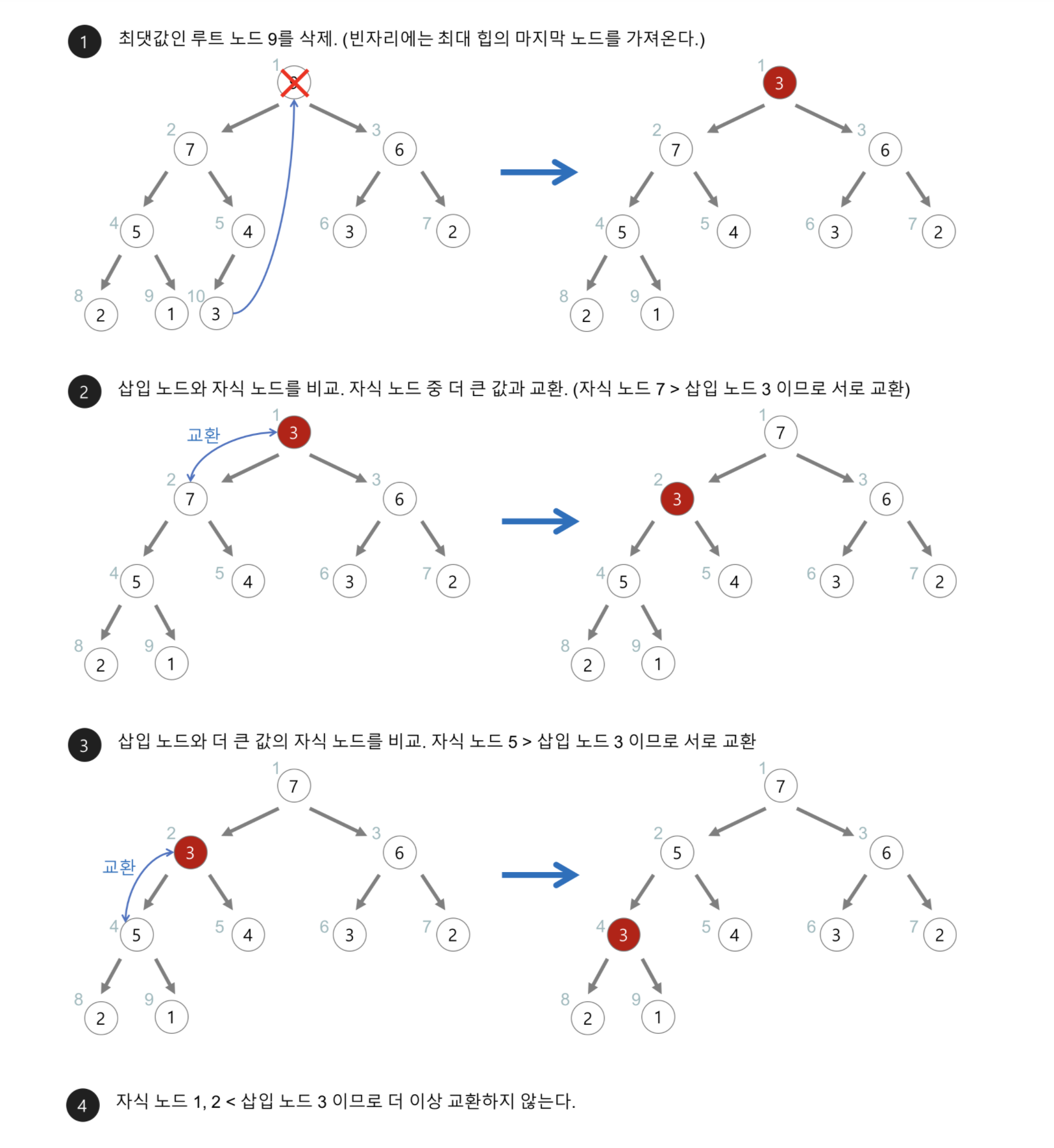
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
- 최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.
- 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
- 힙을 재구성한다.
- 아래의 최대 힙(max heap)에서 최댓값을 삭제해보자.
- 시간 복잡도: O(logN)
Python에서의 힙
Python은 heapq모듈을 통해 heapq를 제공합니다. minheap으로 구현되어 있어 가장 앞에 있는 원소가 가장 작은 원소입니다.
heapq - heapify
- heapq 모듈의 heapify 함수는 주어진 리스트를 힙 정렬합니다. 이때의 Time Complexity는 O(nlongn)입니다.
# 힙 정렬 예시
import heapq
my_list = [13, 2, 1, 5, 10]
heapq.heapify(my_list)
# 가장 작은 원소인 1이 가장 앞으로 왔습니다.
my_list # [1, 2, 13, 5, 10]
heap - heappop(heap)
- heap모듈의 heappop 함수는 힙 정렬된 리스트에서
- 가장 작은 원소를 빼내고
- 나머지 원소가 힙을 유지하도록 정리합니다.
- 이 함수를 사용할 때에는 주어진 리스트가 힙 정렬되어 있는지 반드시 확인해야 합니다.
- 정렬되지 않은 리스트에 heappop을 사용하면 이상한 결과가 나옵니다.
import heapq
my_list = [13, 2, 1, 5, 10]
heapq.heapify(my_list)
# 가장 작은 원소인 1이 리턴됩니다. my_list의 길이가 하나 줄어듭니다.
ret_val = heapq.heappop(my_list)
print("리턴된 값:", ret_val) # 1
print("남은 원소:", my_list) # [2, 5, 13, 10]
heap - heappush(heap, item)
- heap모듈의 heappush 함수는 힙 정렬된 리스트의 힙 상태를 유지하면서 데이터를 삽입시켜줍니다.
- 이 함수를 사용할 때에는 주어진 리스트가 힙 정렬되어있는지 반드시 확인해야 합니다.
- 정렬되지 않은 리스트에 heappush를 사용하면 이상한 결과가 나옵니다.
import heapq
my_list = [13, 2, 1, 5, 10]
heapq.heapify(my_list)
# -1 삽입
heapq.heappush(my_list, -1)
# 가장 작은 원소인 -1이 가장 앞에 위치
print("남은 원소:", my_list) # [-1, 2, 1, 5, 10, 13]
Python으로 힙 구현하기
# Implementing "Max Heap"
class MaxHeap:
def __init__(self, heapSize):
# Create a complete binary tree using an array
# Then use the binary tree to construct a Heap
self.heapSize = heapSize
# the number of elements is needed when instantiating an array
# heapSize records the size of the array
self.maxheap = [0] * (heapSize + 1)
# realSize records the number of elements in the Heap
self.realSize = 0
# Function to add an element
def add(self, element):
self.realSize += 1
# If the number of elements in the Heap exceeds the preset heapSize
# print "Added too many elements" and return
if self.realSize > self.heapSize:
print("Added too many elements!")
self.realSize -= 1
return
# Add the element into the array
self.maxheap[self.realSize] = element
# Index of the newly added element
index = self.realSize
# Parent node of the newly added element
# Note if we use an array to represent the complete binary tree
# and store the root node at index 1
# index of the parent node of any node is [index of the node / 2]
# index of the left child node is [index of the node * 2]
# index of the right child node is [index of the node * 2 + 1]
parent = index // 2
# If the newly added element is larger than its parent node,
# its value will be exchanged with that of the parent node
while (self.maxheap[index] > self.maxheap[parent] and index > 1):
self.maxheap[parent], self.maxheap[index] = self.maxheap[index], self.maxheap[parent]
index = parent
parent = index // 2
# Get the top element of the Heap
def peek(self):
return self.maxheap[1]
# Delete the top element of the Heap
def pop(self):
# If the number of elements in the current Heap is 0,
# print "Don't have any elements" and return a default value
if self.realSize < 1:
print("Don't have any element!")
return -sys.maxsize
else:
# When there are still elements in the Heap
# self.realSize >= 1
removeElement = self.maxheap[1]
# Put the last element in the Heap to the top of Heap
self.maxheap[1] = self.maxheap[self.realSize]
self.realSize -= 1
index = 1
# When the deleted element is not a leaf node
while (index <= self.realSize // 2):
# the left child of the deleted element
left = index * 2
# the right child of the deleted element
right = (index * 2) + 1
# If the deleted element is smaller than the left or right child
# its value needs to be exchanged with the larger value
# of the left and right child
if (self.maxheap[index] < self.maxheap[left] or self.maxheap[index] < self.maxheap[right]):
if self.maxheap[left] > self.maxheap[right]:
self.maxheap[left], self.maxheap[index] = self.maxheap[index], self.maxheap[left]
index = left
else:
self.maxheap[right], self.maxheap[index] = self.maxheap[index], self.maxheap[right]
index = right
else:
break
return removeElement
# return the number of elements in the Heap
def size(self):
return self.realSize
def __str__(self):
return str(self.maxheap[1 : self.realSize + 1])
if __name__ == "__main__":
# Test cases
maxHeap = MaxHeap(5)
maxHeap.add(1)
maxHeap.add(2)
maxHeap.add(3)
# [3,1,2]
print(maxHeap)
# 3
print(maxHeap.peek())
# 3
print(maxHeap.pop())
# 2
print(maxHeap.pop())
# 1
print(maxHeap.pop())
maxHeap.add(4)
maxHeap.add(5)
# [5,4]
print(maxHeap)
Reference
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
