프로그래머스 기지국설치

문제

N개의 아파트가 일렬로 쭉 늘어서 있습니다. 이 중에서 일부 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 기술이 발전해 5g 수요가 높아져 4g 기지국을 5g 기지국으로 바꾸려 합니다. 그런데 5g 기지국은 4g 기지국보다 전달 범위가 좁아, 4g 기지국을 5g 기지국으로 바꾸면 어떤 아파트에는 전파가 도달하지 않습니다.

예를 들어 11개의 아파트가 쭉 늘어서 있고, [4, 11] 번째 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 만약 이 4g 기지국이 전파 도달 거리가 1인 5g 기지국으로 바뀔 경우 모든 아파트에 전파를 전달할 수 없습니다. (전파의 도달 거리가 W일 땐, 기지국이 설치된 아파트를 기준으로 전파를 양쪽으로 W만큼 전달할 수 있습니다.)

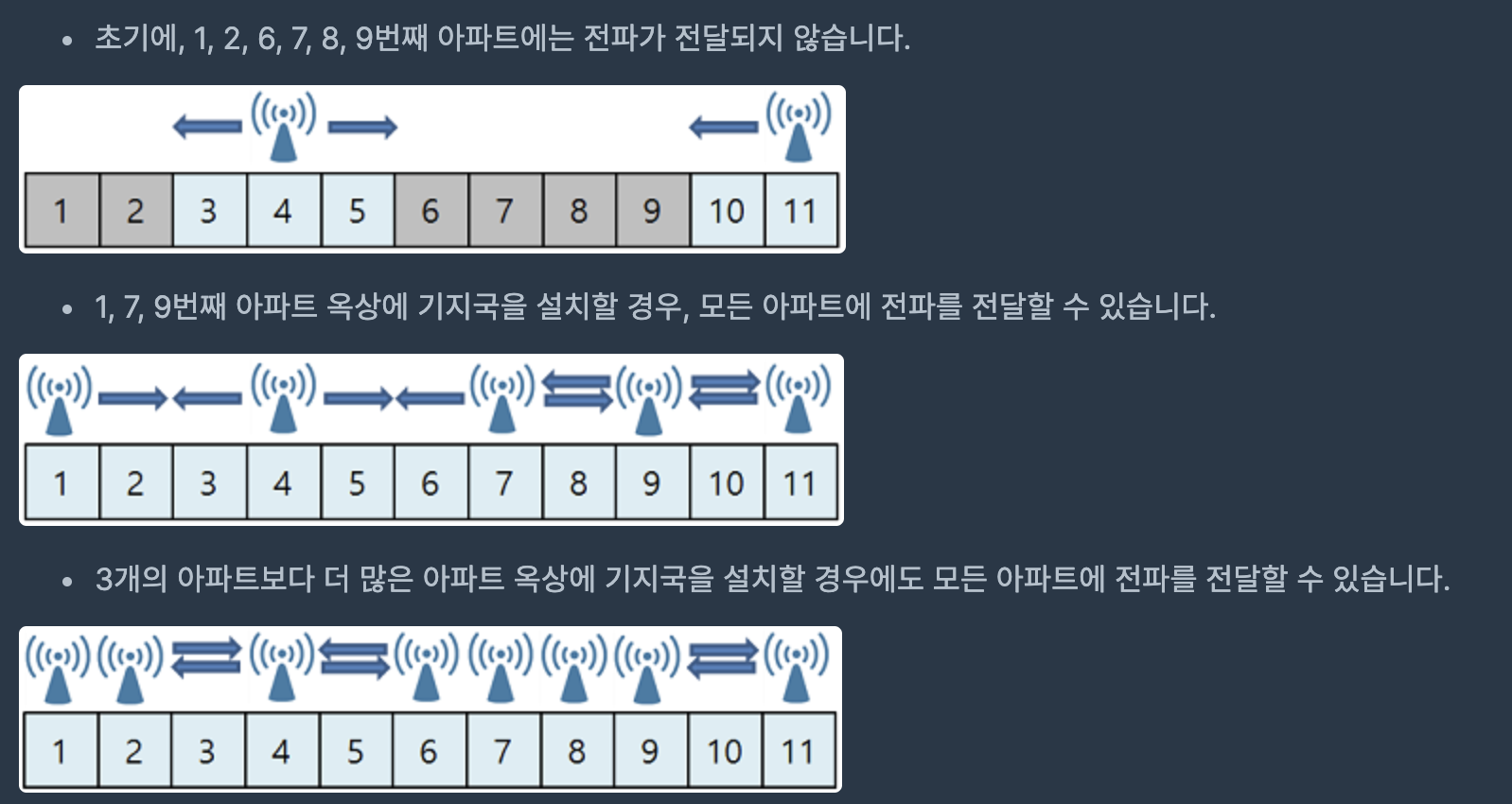
이때, 우리는 기지국을 최소로 설치하면서 모든 아파트에 전파를 전달하려고 합니다. 위의 예시에선 최소 3개의 아파트 옥상에 기지국을 설치해야 모든 아파트에 전파를 전달할 수 있습니다.

아파트의 개수 N, 현재 기지국이 설치된 아파트의 번호가 담긴 1차원 배열 stations, 전파의 도달 거리 W가 매개변수로 주어질 때, 모든 아파트에 전파를 전달하기 위해 증설해야 할 기지국 개수의 최솟값을 리턴하는 solution 함수를 완성해주세요

제한사항

• N: 200,000,000 이하의 자연수
• stations의 크기: 10,000 이하의 자연수
• stations는 오름차순으로 정렬되어 있고, 배열에 담긴 수는 N보다 같거나 작은 자연수입니다.
• W: 10,000 이하의 자연수

입출력 예

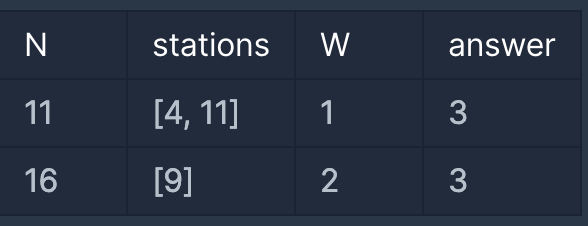
입출력 예 설명

문제에 나온 예와 같습니다.

풀이

정확히 탐욕법이라고 표현하기는 애매하지만, 한번의 반복 안에 최선의 선택을 하기 떄문에 탐욕으로 보였습니다. 이 문제의 핵심은 기지국 설치로 cover되지 못한 부분들을 찾는 것입니다.

• answer 를 0으로 선언
• 기지국 설치로 커버할 수 있는 범위인 width를 2*w+1로 선언
• 기지국이 커버한 범위를 covered 변수로 할당합니다. 처음에는 0으로 선언합니다.
• 각 station을 돌면서 lower = station - w, upper = station + w로 둡니다.
  • 만약 covered가 lower보다 작거나 같다면, 기지국이 커버를 못한 범위가 있는 것.
  • 기지국을 설치할 수 있는 최솟값을 구하고 answer에 더합니다. (이때 math 라이브러리의 ceil함수를 불러와 적용)
  • ex) 범위가 5인 경우, width가 5이면 1개 설치로 충분. 범위가 6인 경우는 2개를 설치해야함. 즉 커버하지 못한 범위를 width로 나눈 후 올림값을 써야함.
  • 기지국 설치 후 covered를 upper로 변경해줌
• station을 다 돌아도 맨 끝부분이 cover되지 않았을 수도 있으므로 n-covered에 대해서 똑같이 적용

import math

def solution(n, stations, w):
    covered = 0
    width = 2 * w + 1
    answer = 0
    for station in stations:
        lower = station - w
        upper = station + w
        if covered <= lower: # 커버하지 못한 부분이 남아있으면
            answer += math.ceil((lower - 1 - covered) / width)
        covered = upper
    if covered <= n: # 커버하지 못한 부분이 남아있으면
        answer += math.ceil((n - covered) / width)


    return answer