[Python] 20057 마법사 상어와 토네이도
20055 마법사 상어와 토네이도
문제
마법사 상어가 토네이도를 배웠고, 오늘은 토네이도를 크기가 N×N인 격자로 나누어진 모래밭에서 연습하려고 한다. 위치 (r, c)는 격자의 r행 c열을 의미하고, A[r][c]는 (r, c)에 있는 모래의 양을 의미한다.
토네이도를 시전하면 격자의 가운데 칸부터 토네이도의 이동이 시작된다. 토네이도는 한 번에 한 칸 이동한다. 다음은 N = 7인 경우 토네이도의 이동이다.
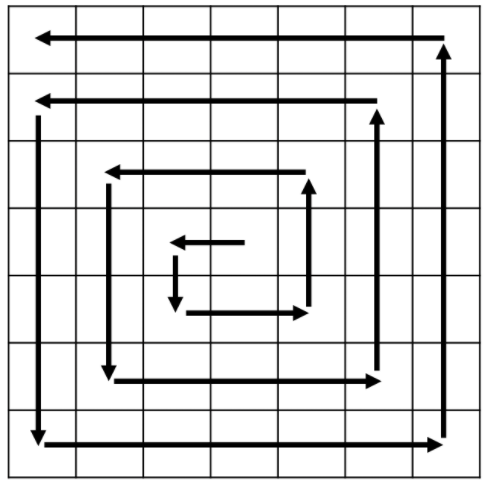
토네이도가 한 칸 이동할 때마다 모래는 다음과 같이 일정한 비율로 흩날리게 된다.
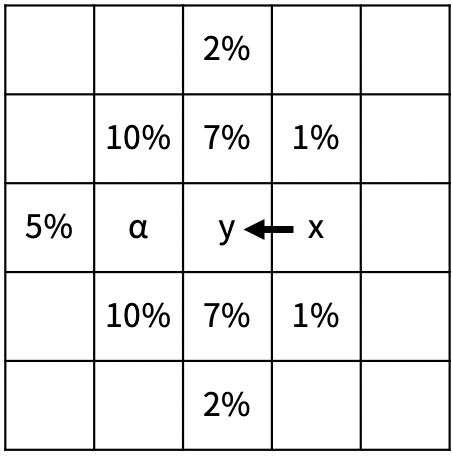
토네이도가 x에서 y로 이동하면, y의 모든 모래가 비율과 α가 적혀있는 칸으로 이동한다. 비율이 적혀있는 칸으로 이동하는 모래의 양은 y에 있는 모래의 해당 비율만큼이고, 계산에서 소수점 아래는 버린다. α로 이동하는 모래의 양은 비율이 적혀있는 칸으로 이동하지 않은 남은 모래의 양과 같다. 모래가 이미 있는 칸으로 모래가 이동하면, 모래의 양은 더해진다. 위의 그림은 토네이도가 왼쪽으로 이동할 때이고, 다른 방향으로 이동하는 경우는 위의 그림을 해당 방향으로 회전하면 된다.
토네이도는 (1, 1)까지 이동한 뒤 소멸한다. 모래가 격자의 밖으로 이동할 수도 있다. 토네이도가 소멸되었을 때, 격자의 밖으로 나간 모래의 양을 구해보자.
입력
첫째 줄에 격자의 크기 N이 주어진다. 둘째 줄부터 N개의 줄에는 격자의 각 칸에 있는 모래가 주어진다. r번째 줄에서 c번째 주어지는 정수는 A[r][c] 이다.
출력
격자의 밖으로 나간 모래의 양을 출력한다.
제한
- 3 ≤ N ≤ 499
- N은 홀수
- 0 ≤ A[r][c] ≤ 1,000
- 가운데 칸에 있는 모래의 양은 0
풀이
- 바람이 부는 방향과 이동 패턴을 어떤식으로 구현할 지
- 바람이 부는 방향에 따라 모래가 퍼지는 비율 이차원 배열을 어떤 식으로 만들지
이 두가지가 핵심입니다.
첫번째의 경우 살펴보면, 토네이도가 이동하는 거리는 1,1,2,2,3,3,4,4… 이며 각 횟수가 끝나면 좌 하 우 상으로 방향이 바뀝니다. 이를 위해 turn 이라는 배열에 [1,1,2,2,3,3,4,4…] 식으로 넣고 그 안의 원소값만큼 for문을 돌립니다. for문이 끝나면 방향을 전환하고 다시 다음 원소값만큼 for문을 돌립니다.
두번쨰의 경우, 오른쪽으로 90도 회전시키는 함수를 구현하였고, 왼쪽 방향으로 sand를 퍼뜨리는 함수만 구현하였습니다. 방향 전환을 할때마다 sand를 그 방향으로 퍼뜨리기 보다는 board를 회전시키는 방법을 사용했습니다. rotate함수 내에서 for문이 2개가 돌기 때문에 pypy3는 통과하나 python3로는 시간초과가 떴습니다. 때문에 rotate 함수를 포기하고 각 방향에 따른 모래 비율을 일일이 구현해주었습니다.
또한 바깥으로 빠지는 모래의 합을 구해야 하기 때문에 board에 가로 세로 각 2칸씩 0으로 된 padding을 넣어주었습니다. 마지막에 padding의 값들을 합쳐주어 결과를 제출하였습니다.
a = int(input())
board = [list(map(int,input().split())) for _ in range(a)]
# 바람의 방향에 따른 모래 비율
rate_left = [[0,0,2,0,0],[0,10,7,1,0],[5,'a',0,0,0],[0,10,7,1,0],[0,0,2,0,0]]
rate_down = [[0,0,0,0,0],[0,1,0,1,0],[2,7,0,7,2],[0,10,'a',10,0],[0,0,5,0,0]]
rate_right = [[0,0,2,0,0],[0,1,7,10,0],[0,0,0,'a',5],[0,1,7,10,0],[0,0,2,0,0]]
rate_up = [[0,0,5,0,0],[0,10,'a',10,0],[2,7,0,7,2],[0,1,0,1,0],[0,0,0,0,0]]
## 가로 세로 2칸씩 padding을 둔다
def padding(board):
nrow = len(board)
board = [[0]*nrow] + [[0]*nrow] + board + [[0]*nrow] +[[0]*nrow]
board = [[0,0]+x+[0,0] for x in board]
return board
def sand(x, y, board, rate):
# board 좌표를 rate 배열과 대응할 수 있도록 좌표이동
a,b = x-2, y-2
temp = 0 # Y에서 빠져 나간 모래의 총 양
for row in range(5):
for col in range(5):
if rate[row][col] != 0 and rate[row][col] != 'a':
board[a+row][b+col] += board[x][y]*rate[row][col]//100
# a의 양을 차후에 계산하기 위해 이동되는 모래의 양을 temp에 저장해둔다.
temp += board[x][y]*rate[row][col]//100
elif rate[row][col] == 'a':
# a의 좌표를 기억한다.
remain = (a+row, b+col)
# 나머지 a 부분 처리
board[remain[0]][remain[1]] += board[x][y] - temp
board[x][y] = 0
return board
board = padding(board)
turn = [x//2 for x in range(2,1000)]
breaker = False # 이중 for문 break를 위한 변수
# 시작점
x = len(board)//2
y = len(board)//2
dir = [(0,-1),(1,0),(0,1),(-1,0)] # 왼 아래 오른쪽 위
dir_ind = 0
# turn을 하는 주기가 [1,1,2,2,3,3,4,4]로 각 횟수가 끝날때마다 방향을 바꿔준다. (dir_ind에 1씩 더해준다.)
for point in turn:
for _ in range(point):
if x==2 and y==2: # 패딩으로 (0,0) 이 아닌 (2,2)이 종착점이 된다.
breaker=True
break
dx, dy = dir[dir_ind%4][0], dir[dir_ind%4][1]
x,y = x+dx, y+dy
if dir_ind%4 == 0:
board = sand(x,y,board, rate_left)
elif dir_ind%4 == 1:
board = sand(x,y,board, rate_down)
elif dir_ind%4 == 2:
board = sand(x,y, board, rate_right)
else:
board = sand(x,y, board, rate_up)
if breaker:
break
dir_ind += 1
## 테두리 더하기
answer = 0
answer += sum([x[0] for x in board])
answer += sum([x[1] for x in board])
answer += sum([x[-1] for x in board])
answer += sum([x[-2] for x in board])
for i in [0,1,len(board)-1, len(board)-2]:
for j in range(2,len(board)-2):
answer += board[i][j]
print(answer)
